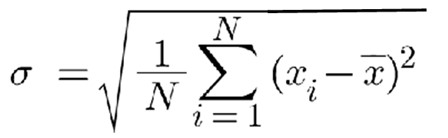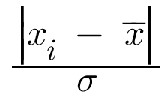| ||||||
|
You may redistribute this newsletter for non-commercial purposes. For commercial use contact jack@ganssle.com. To subscribe or unsubscribe go here or drop Jack an email. |
||||||
| Contents | ||||||
| Editor's Notes | ||||||
|
Tip for sending me email: My email filters are super aggressive and I no longer look at the spam mailbox. If you include the phrase "embedded" in the subject line your email will wend its weighty way to me. Coming soon: 1 trillion transistor GPUs. |
||||||
| Quotes and Thoughts | ||||||
|
In times of change learners inherit the earth while the learned find themselves beautifully equipped to work in a world that no longer exists. - Eric Hoffer |
||||||
| Tools and Tips | ||||||
|
Please submit clever ideas or thoughts about tools, techniques and resources you love or hate. Here are the tool reviews submitted in the past. Daniel McBrearty has a nice way to improve the use of assert():
Ingo Marks sent this update:
|
||||||
| Rejecting Outliers | ||||||
|
We often average input data to reject noise and get a more accurate model of the data we're sampling. In some cases naive averaging can lead to unacceptable errors. A single data point wildly out of range can skew the mean, giving us quite incorrect results. One solution is to reject outliers before computing the average. There are many ways to do this. A simple approach is sigma clipping. Compute the standard deviation of the data and reject samples with a sigma greater than some value. (That number is very application dependent). This is simple and fast. In the absence of hardware floating point one could dispense with the computationally-expensive square root, which yields the variance. However, I generally prefer standard deviation over variance, as the former is in the same units as the data. If you're measuring length in meters, standard deviation is also in meters. Don't want to toss data? An alternative is Winsorized sigma clipping (named for statistician Charles Winsor). Instead of rejecting outliers, replace them with an adjacent value. For instance, if the data looks like: 24, 25, 22, 20, 28, 102, 23, 25, 31, 22, 23 Replace the outlier with an adjacent data point - perhaps the one to the right: 24, 25, 22, 20, 28, 23, 23, 25, 31, 22, 2 ... again, using the standard deviation to identify outliers. Sure, this is a bit of a lie as we're making up data. But it's a white lie that won't skew the result. For the last year or two I've been using a newish-to-me method of rejecting outliers. It goes by the unwieldly name "Generalized Extreme Studentized Deviate" (often abbreviated ESD), which sounds like something an academic would make a career of, but is pretty simple in concept. Compute the mean and standard deviation of the set of samples. Then find the sample for which: is a maximum. Remove that sample from the dataset. Recompute the mean and standard deviation and repeat. Continue removing samples until you've removed however many outliers you expect. A better stopping criteria is to monitor the change in the size of that equation, and stop when it falls below some value. Again, I'd use the standard deviation here. I am no statistician, but suspect one could remove the divisor, as that is a constant. You still want the standard deviation to compute a stopping criteria, but could compute the subtraction at the same time as figuring sigma. A more complex alternative is detailed here. I've found that ESD is remarkably effective at removing very strong signals that should not be part of the data set. It's computationally expensive, but may be an option when there are sufficient CPU cycles. |
||||||
| Mean or Median? | ||||||
|
When running statistics should we use the mean or median? Generally we default to the mean, which more often than not makes sense. Sometimes we'll average just out of habit. But when the mean and median are very different it may make sense to profile using the latter. Here in the little unincorporated town of Finksburg, MD we have a population of about 10,000. I imagine the average salary is around $100k, with a similar median. In other words, most folks here probably get a more or less Gaussian distribution around $100k; some a bit more, others somewhat less. If Elon Musk moved into one of our modest houses, though, Finksburg's mean income jumps to millions of dollars - even though (I imagine) no one earns anything like that. The median hasn't changed and is much more representative of the town's income. One could argue that the mean is still a good model if we reject Musk as an outlier (see above). But outliers are sometimes where the interesting data lies. Consider a picture of a remote galaxy. The sky is nearly black; virtually all of the data is the blackness at the left side of a histogram. A tiny percentage of the pixels are bright - the stars we're focused on. That's the interesting stuff, yet those pixels might represent a faction of a percent of all of the data. They look like outliers but are not. As always, know your data before deciding how to process it. |
||||||
| More on Engineering Ethics | ||||||
|
Responding to last issue's take on engineering ethics, Greg Hansen notes the Ritual of the Calling of An Engineer, which has been an institution in Canada for a long time. From the Wikipedia article:
Dave Telling wrote:
Tom Lock
|
||||||
| Failure of the Week | ||||||
Dainius Stankevicius wrote: The discount percentage somehow managed to become a NaN. Although when one compares the two posters, we can see that the poster on the left uses commas while the one on the right uses points, which most likely was the reason. But still, someone had to print it and physically put it up there... And this is from Chris Hammond: Have you submitted a Failure of the Week? I'm getting a ton of these and yours was added to the queue. |
||||||
| Jobs! | ||||||
|
Let me know if you’re hiring embedded engineers. No recruiters please, and I reserve the right to edit ads to fit the format and intent of this newsletter. Please keep it to 100 words. There is no charge for a job ad. |
||||||
| Joke For The Week | ||||||
These jokes are archived here. If C++ is so good why has it never improved to A+? |
||||||
| About The Embedded Muse | ||||||
|
The Embedded Muse is Jack Ganssle's newsletter. Send complaints, comments, and contributions to me at jack@ganssle.com. The Embedded Muse is supported by The Ganssle Group, whose mission is to help embedded folks get better products to market faster. |