Chaotic Systems

The new science of chaos is fascinating in its own right, and may have important implications for designers of embedded systems.

Published in Embedded Systems Programming, March, 1995

By Jack Ganssle

"Everything you know is wrong". This quote, from a 60s-era Firesign Theater album, sums up my feelings about sliding into middle age, with life relentlessly hammering away in one direction and the kids constantly reminding me of various inadequacies. At least I can fall back on the determinism and certainty of digital systems.

Or, can I? Science took a very unexpected twist in this century. The reductionist approach advocated by Descartes and so many others (i.e., "understand the parts and then you'll understand the whole") was first assailed by Bohr and pals with their introduction of quantum mechanics. Heisenburg pounded another nail in reductionism's coffin by proving we'll never really be able to measure all of the bits and pieces of atomic events.

James Lovelock's concept of Gaia, at the very least a tremendously fascinating philosophical exercise, forced us to look at systems from the top down. Part of his hypothesis implies that biological environments are so tremendously complex that understanding comes only from examining them on a macroscopic scale. That is, we'll never derive the wonderfully intricate effects of life on the environment by studying nothing more than cellular structures; we have to look at the entire biosphere as a whole. In fact, as NASA prepared to send a billion dollars of Viking hardware to Mars to look for life by analyzing soil for animo acids, Lovelock correctly (?) predicted life's absence by noting there is no oxygen in the planet's atmosphere. An effect of life, Lovelock contends, is a macroscopic change in the environment.

Now the emerging science of complexity -- popularly called "chaos theory" -- undermines even our understanding of the behavior of simple algebraic equations. Here's the bad news: iterative solutions of many of the very simplest of polynomials can give results that apparently make no sense.

A Quick Overview

Perhaps you've heard statements from the popular press claiming that the weather is inherently unpredictable because the flapping of a butterfly's wings in Brazil will ultimately have some effect in your own home town. The essence of this statement is that we can never, ever, know the initial conditions of a system with enough precision to predict its outcome. Remember that Heisenberg told us that the act of measurement effects the result, limiting the resolution of any instrument we care to use to get this initial data. If your system is wildly dependent on the starting point, the limits imposed by quantum mechanics will give us wild results.

Our brains understand linear systems. Make a little change in the input and you naturally anticipate a small change in the output results. The effects of quantum uncertainties are so far down in the noise as to be unimportant. Unfortunately, most of the world is inherently non-linear, and in many non-linear systems the output is sensitively dependent on initial conditions.

In 1961 Edward Lorenz, while studying weather simulations, found that one of his equations behaved most oddly. He predicted that the parameter X was a function of its state at some early time, and related X' (the new value of X) to X by:

X'=AX(1-X)

(This is the same equation used by population biologists to predict the number of animals in an area in successive generations).

Lorenz had his primitive computer run numbers through his equation repeatedly, at each stage substituting the last computed X' into X. He found that as long as the constant A remained small X' converged to a result that was proportional to the value of A. You'd expect this. If the result monotonically diverged to infinity your sense of proportion would be equally satisfied.

When A gets near the value 3 the equation gives results that simply make no sense. For an identical A and X, iterating the equation will converge to one of two results. Increase A to about 3.5 and the same iterations yields four results. As A gets just a bit larger the complexity of the result soars, with millions, then billions, of answers... all for the same input data!

In Lorenz's case, he found that limited floating point precision created tiny errors responsible for the apparently crazy concept that one equation with one set of data could yield many answers. However, it turns out that for any finite amount of floating point precision the equation will still eventually degenerate into this "chaotic" region, chaos meaning "pretty good data in, crazy stuff out".

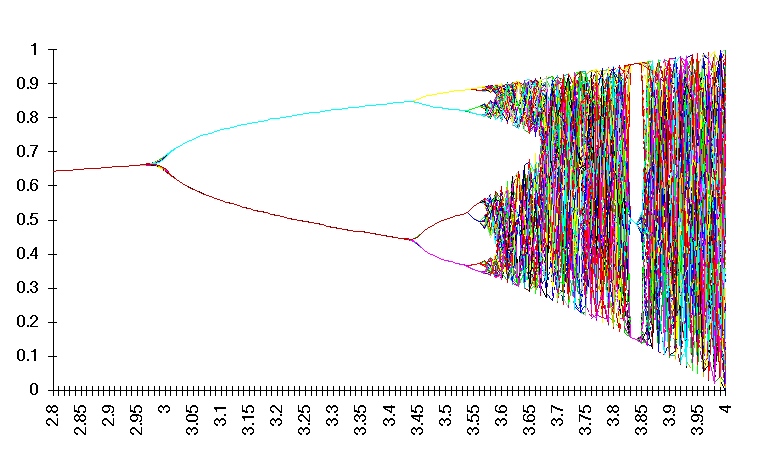
The figure shows a dramatic view of the descent of the equation into chaos. The horizontal axis is "A" - the polynomial coefficient. The vertical axis shows X'. I created the plot with a simple (but huge!) Excel spreadsheet. For A less than 3 or so the result is like that of a traditional function: a single value in results in a single value out. Above 3 the curve forks into two result for each value of A. At about 3.45 the curve forks again, a process that repeats until an infinite number of answers appear.

Mathematicians call this repeated forking "period doubling". It's a common characteristic of chaotic systems.

Chaos and Us

It's easy to dismiss chaos as a result of Lorenz's odd equation. Few of our systems use equations of this form... or do they?

Lorenz's equation is nothing more than a simple second-order polynomial. It's equivalent to:

X'=AX-AX2

or,

X'=-AX2 + BX + C

where A=B

where C is zero, though in fact any value of C will give a chaotic result.

iterated second degree polynomial is identical to Lorenz's ill-behaved equation!

Further research showed that chaos is a characteristic of non-linear equations of any degree. If your product iterates a polynomial, beware!

Iterating is one of the things computers do best, and is a standard part of any programmer's repertoire. Iteration is nothing more than feedback, one of the most commonly-used techniques in analog circuit design. Are we building systems grounded in mathematical quicksand?

So, gentle reader, I pose a question: how sure are you that your new product, that instrument using a micro to solve a series of equations, operates in a non-chaotic region? As a mathematics amateur I'll plead ignorance to the fine details of chaos. It's clear, though, that simple equations are rife with scary behavior, behavior we can ignore only at our own (and our customers') peril.

I think that our industry needs to examine the implications of this theory for our products. Let's face it: while scores of mathematicians develop beautiful theories to explain and manipulate chaos, we, who write the code that makes the computers iterate, are basically ignorant of its implications.

Iterations

I invite someone with mathematical authority to email in with an explanation of what sort of conditions we should watch out for. In the meantime I'd be wary of any non-linear algorithm - particularly one that iterates.

In a former life I worked on machines that computed the percentage protein in wheat by measuring the amount of IR energy reflected from a grain sample. Reflectances from numerous wavelengths all contributed to the protein result in a complex manner, all combined in a polynomial whose coefficients were determined by a tedious iterative process much like that described above. Quite often the coefficients gave an equation that predicted wildly erratic protein values. At the time we called these "bad calibrations" and blithely advised users to repeat the experiment, but now I suspect the instruments operated on the edge of chaos.

In another situation, my former partner and I designed steel thickness measuring equipment. The units were self-calibrating: the software tossed various known thicknesses of steel into the x-ray beam, and then computed a least squares solution to a polynomial which would predict the thickness of any piece of the same material. Though the system worked pretty well, it was horribly sensitive to changes in practically any parameter. Not supplying enough known-thickness pieces resulted in crummy predictive powers of the polynomial, as did any tiny error in the standards. We developed empirical procedures that generally resulted in good results... but never understood the why behind the what.

Now I wonder how much sense it makes to let a system automatically compute coefficients of a polynomial of two or higher degree. If you know the coefficients then you can probably model the system to see if there is a tendency to degenerate into chaos. When the computer picks the coefficients, anything goes.

Just how does one go about modeling potential chaos? I've been building simulations using spreadsheets. For a polynomial like Lorenz's this is easy: put slowly increasing hard-coded values of A along the columns, and then iterations down the rows. Plot the columns and look for values that do not converge to a single answer.

It's a bit harder to do this for equations of higher degree with so many more coefficients. Perhaps a better approach is a simple C simulation of the equation that looks for chaos as the coefficients are diddled around the values the system will use.

I'd be wary of running this experiment on a Pentium! Offload the divisions to a coprocessor... or even a software floating point emulation running on a good old reliable 8051. Those pesky Pentium division problems will seed all sorts of errors into your results.

Questions

Any non-linear system could be chaotic. Reference (3) includes a chapter about predicting chaos, but it's far over my head. I invite responses from anyone having experience or thoughts about this.

A collerary of this could be: how close can we ride to the edge of a known chaotic condition. In the case of the Lorenz equation it's just a matter of knowing at what point A causes the system to degenerate. When two, three or more variables are involved, what do we do?

At the risk of admitting even more ignorance, some day I'd like to understand the process of how a system falls into chaos. If you maintain 80 bits of floating point precision, can the system stand twice the iterations as with 40 bit precision? I'm looking for an infinite-precision BCD math package that will let me study this. I'll report on the results... when there are some.

Know-it-Alls

I advise every embedded software person to start studying chaos. Given that it has such profound effects on even the simplest equation, there's a chance you could spend a lot of time fighting what appears to be a software bug but is in fact an artifact of the math.

It reminds me of trying to debug a system years ago that measured absorption of oils in perclorethelene. Nothing worked; I spent weeks looking fruitlessly for the problem. A chemist who fortuitously dropped by explained that the effect I was looking for was swamped by minute amounts of alcohol in the solvent.

The embedded world is truly interdisciplinary. You have to be partly a hardware designer, partly a firmware guru, a chemist, radiologist, and part Renaissance man (ah, person). If the system computes mathematical solutions, you better study bone up on math as well. What you don't know can, and will, bite you.

Read widely.

References:

1. Chaos, the Making of a New Science, by James Gleick, 1987, R. R. Donnelley & Sons Company, Harrisonburg, VA - This is a must-read for any educated person. I couldn't put it down.

2. Exploring Chaos, by Nina Hall, 1991, W. W. Norton & Company, NY, NY. You have to read this one. Chapter 12, Chaos, Catastrophes and Engineering, covers chaotic failures in real life. Chapter 13, Chaos on the circuit board, cuts uncomfortably close to home for most of us.

3. Chaos, by Arun Holden, 1986, Princeton University Press, Princeton, NJ. The math makes this a hard read for those of us suffering from calculus withdrawal. Still, there's a lot of useful information to be had here. Various chapters discuss chaos in everyday life, from electronic feedback to cardiac rhythms.

4. Newton's Clock, by Ivars Peterson, 1993, W. H. Freeman and Company, NY, NY. The universe seems held together by chaos, as this book describes so well. There are important islands of stability in chaotic systems, which explain the motion of many of the solar system's moons.

5. The Turbulent Mirror, by John Briggs and F. David Peat, 1989, Harper & Row, NY, NY. A fascinating, very readable account of chaos.

6. Ages of Gaia, by James Lovelock, 1988, W. W. Norton & Company, NY, NY. This is the best of the Gaia books, from the one who started it all.