If you don't know about V(G) your code could be at risk.

A few years ago I wrote about Defect Removal Efficiency, a must-track metric that tells us how effectively we're removing bugs. I showed that tracking this is a sure way to improve the quality of the code you're shipping.

Some other metrics are important, too.

Code complexity is easy to measure and a sure-fire way to assess the quality of the code. "Complexity" is a vague term; there are really two kinds. One is a product's essential complexity, or the difficulty of the problem being solved. A dumb thermostat falls at the bottom of the spectrum while a smart phone is inherently a very big and complex application. Essential complexity tells us little about code quality.

Internal complexity tells us how well we've implemented the functionality. There are a lot of metrics for this, but by far the most common is McCabe Cyclomatic Complexity. The name is somewhat terrifying and sounds like a professor's grab for grant money. But McCabe refers to Tom McCabe, who proposed the metric, and cyclomatic to the graph theory it's based on.

Don't be scared off by the pompous name. The idea is trivially simple. Cyclomatic complexity, known as V(G), is measured on a function by function basis, and is simply the number of paths through a function. Does one comprise nothing more than 30 assignment statements? If so, there's only one way the code can traverse the function so the complexity is one. Add a simple if statement and now there are two paths, so V(G)=2.

Why is this important? It has been shown that a function with a complexity of ten or less is of low risk and likely to be correct. As the number grows risk increases; a function scoring 20 or more is high-risk. At 50 a function is considered untestable.

Think of that: untestable.

Examples:

  • I ran 3.3 million lines of the Linux kernel through a complexity tool. The 161,000 functions averaged 4.94. Since under 10 is good, this is a fantastic result. However, 722 functions scored in the untestable, over 50, range. One of those is a driver with 2281 lines of code (in one function!) which scored a Frankensteinien 352. And only 3.7% of the statements were or had comments. (I have data showing the best code scores 60-70% comments).
    • FreeRTOS is a great RTOS whose code base has been used in safety critical systems. The average function's complexity is 3.44. Only one function scored over ten, and just barely at 11.

    eCos, another reliable RTOS, averages an astounding 2.54. Three percent of the functions exceed ten, but none is more than 18.

    There's a critical corollary to cyclomatic complexity. V(G) is the minimum number of tests needed to show that a function is correct. It says nothing about the max; one whose complexity is 5 may need 50 tests. But at least it gives us a lower bound, a metric we can hold our tests to. If you've run 4 tests against that code, then it has not been properly tested. Period.

    Do you hold your tests to any sort of analytical standard? Few do, but cyclomatic complexity gives us one end of a bounds check.

    Sometimes V(G) can be foxed. The following statement's complexity is 2 since there are only two paths that can be taken. But clearly a lot of tests would be needed to exercise it properly:

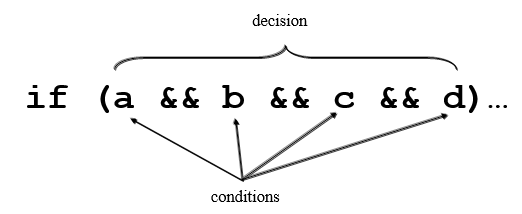
    A compound if statement

    The DO-178C avionics standard, for level A code (the most safety-critical) requires "modified condition/decision coverage" (MC/DC) tests. This means:

    • Every decision has taken every possible outcome
    • Every condition takes every possible outcome
    • Each condition is shown to independently affect the outcome

    So cyclomatic complexity is an imperfect predictor of testing. But it's a good rough guide. In engineering we use numbers to guide our work, accepting that they may be imperfect.

    What about switch statements? Every case adds one to the V(G). Yet sometimes a monster switch is the clearest way to express an idea. Many in academia make no exceptions, but I feel switch statements should be excluded from these calculations. Get the numbers and then evaluate them using your engineering judgement.

    My take is this: We know functions with high V(G) add risks. Routinely run a complexity analyzer over your code and investigate functions with high scores. Recode as appropriate. Very often a big number indicates the developer wrote confusing code that can be simplified. Or he was confused while writing the code, so clarity and accuracy suffers.

    Complexity is at the heart of basis path testing, an idea that insures all possible paths do get tested. That is pretty much impractical for us. Or, at least when done manually. But tools can do it; some exist that will do the analysis and automatically construct unit tests that test every possible direction the code can go, including all MC/DC permutations.

    I have seen one of these tools generate 50k lines of code to test a 10k LOC program.

    How many of us construct such comprehensive tests?

    Tools to measure complexity abound. Here's a freebie that is quite good.

    Published July, 2016